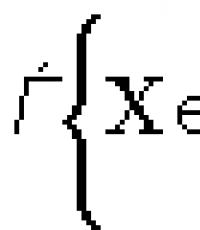Задачи с решениями. Геометрическое определение вероятности. Задачи с решениями

План-конспект разработанный

Геометрическая вероятность

Цели и задачи: 1) Познакомить учащихся с одним из возможных способов задания

вероятности;

2) Повторение пройденного и закрепление навыков формализации

текстовых вероятностных задач с помощью геометрических фигур.

Результаты обучения:

1) Знать определение геометрической вероятности выбора точки

внутри фигуры на плоскости и прямой;

2) Уметь решать простейшие задачи на геометрическую вероятность,

зная площади фигур или умея их вычислять.

I . Выбор точки из фигуры на плоскости.

Пример 1. Рассмотрим мысленный эксперимент: точку наудачу бросают на квадрат, сторона которого равна 1. Спрашивается, какова вероятность события, которое состоит в том, что расстояние от этой точки до ближайшей стороны квадрата не больше чем ?

В этой задаче речь идет о так называемой геометрической вероятности.

Точку наудачу бросают в фигуру F на плоскости. Какова вероятность того, что точка попадает в некоторую фигуру G, которая содержится в фигуре F.

Ответ зависит от того, какой смысл мы вкладываем в выражение «бросить точку наудачу».

Обычно это выражение трактуют так:

1. Брошенная точка может попасть в любую часть фигуры F.

2. Вероятность того, что точка попадает в некоторую фигуру G внутри фигуры F, прямо пропорциональна площади фигуры G.

Подведем итог: пусть и - площади фигур F и G . Вероятность события А «точка Х принадлежит фигуре G, которая содержится в фигуре F », равна

Заметим, что площадь фигуры G не больше, чем площадь фигуры F, поэтому

Вернемся к нашей задаче. Фигура F в этом примере квадрат со стороной 1. Поэтому =1.

Точка удалена от границы квадрата не более чем на , если она попала в заштрихованную на рисунке фигуру G. Чтобы найти площадь , нужно из площади фигуры F вычесть площадь внутреннего квадрата со стороной .

Тогда вероятность того, что точка попала в фигуру G, равна

Пример 2. Из треугольника АВС случайным образом выбирается точка Х. Найти вероятность того, что она принадлежит треугольнику, вершинами которого являются середины сторон треугольника.

Решение: Средние линии треугольника разбивают его на 4 равных треугольников. Значит,

Вероятность того, что точка Х принадлежит треугольнику KMN, равна:

Вывод. Вероятность попадания точки в некоторую фигуру прямо пропорциональна площади этой фигуры.

Задача. Нетерпеливые дуэлянты.

Дуэли в городе Осторожности редко кончаются печальным исходом. Дело в том, что каждый дуэлянт прибывает на место встречи в случайный момент времени между 5 и 6 часами утра и, прождав соперника 5 минут, удаляется. В случае же прибытия последнего в эти 5 минут дуэль состоится. Какая часть дуэлей действительно заканчивается поединком?

Решение: Пусть х и у обозначают время прибытия 1-го т 2-го дуэлянтов соответственно, измеренное в долях часа начиная с 5 часов.

Дуэлянты встречаются, если , т. е. x - < y < x + .

Изобразим это на чертеже.

Заштрихованная часть квадрата отвечает случаю, когда дуэлянты встречаются.

Площадь всего квадрата 1, площадь заштрихованной части:

Значит, шансы на поединок равны .

II . Выбор точки из отрезка и дуги окружности.

Рассмотрим мысленный эксперимент, который состоит в случайном выборе одной точки Х из некоторого отрезка MN.

Это можно понимать так, будто точку Х случайным образом «бросают» на отрезок. Элементарным событием в этом опыте может стать выбор любой точки отрезка.

Пусть отрезок CD содержится в отрезке MN. Нас интересует событие А , состоящее в том, что выбранная точка Х принадлежит отрезку CD.

Метод вычисления этой вероятности тот же, что для фигур на плоскости: вероятность пропорциональна длине отрезка CD.

Следовательно, вероятность события А «точка Х принадлежит отрезку CD, содержащемуся в отрезке MN» равна, .

Пример 1. Внутри отрезка MN случайным образом выбирается точка Х. Найдите вероятность того, что точка Х ближе к точке N, чем к M.

Решение: Пусть точка О – середина отрезка MN. Наше событие наступит тогда, когда точка Х лежит внутри отрезка ON.

Тогда .

Ничего не меняется, если точка Х выбирается не из отрезка, а из дуги некоторой кривой линии.

Пример 2. На окружности даны точки А и В, причем эти точки не являются диаметрально противоположными. На этой же окружности выбирается точка С. Найти вероятность того, что отрезок ВС пересечет диаметр окружности, проходящий через точку А.

Решение: Пусть длина окружности равна L. Интересующее нас событие К «отрезок ВС пересекает диаметр DA» наступает, только если т. С лежит на полуокружности DA, не содержащей точку В. Длина этой полуокружности равна L.

Пример 3. На окружности взята точка А. На окружность «бросают» точку В. Какова вероятность того, что длина хорда АВ будет меньше радиуса окружности.

Решение: Пусть r – радиус окружности.

Для того чтобы хорда АВ была короче радиуса окружности, точка В должна попасть на дугу В1АВ2, длина которой равна длины окружности.

Вероятность того, что длина хорды АВ будет меньше радиуса окружности, равна:

III . Выбор точки из числового отрезка

Геометрическую вероятность можно применять к числовым промежуткам. Предположим, что случайным образом выбирается число Х, удовлетворяющее условию . Этот опыт можно заменить опытом, в котором из отрезка на числовой прямой выбирается точка с координатой Х.

Рассмотрим событие, состоящее в том, что точка с координатой Х выбрана из отрезка , содержащегося в отрезке . Это событие обозначим . Его вероятность равна отношению длин отрезков и .

Пример 1. Найти вероятность того, что точка, случайно выбранная из отрезка , принадлежит отрезку .

Решение: По формуле геометрической вероятности находим:

Пример 2. Согласно правилам дорожного движения, пешеход может перейти улицу в неустановленном месте, если в пределах видимости нет пешеходных переходов. В городе Миргороде расстояние между пешеходными переходами на улице Солнечной равно 1 км. Пешеход переходит улицу Солнечную где-то между двумя переходами. Он может видеть знак перехода не дальше чем за 100 м от себя. Найдите вероятность того, что пешеход не нарушает правила.

Решение: Воспользуемся геометрическим методом. Расположим числовую прямую так, что участок улицы между переходами окажется отрезком . Пусть пешеход подходит к улице в некоторой точке с координатой Х. Пешеход не нарушает правила, если он находится на расстоянии более чем 0,1 км от каждого перехода, т. е. 0,1

Пример 3. Поезд проходит мимо платформы за полминуты. В какой-то момент, совершенно случайно выглянув из своего купе в окно, Иван Иванович увидел, что поезд идет мимо платформы. Иван Иванович смотрел в окно ровно 10 секунд, а затем отвернулся. Найдите вероятность того, что он видел Ивана Никифоровича, который стоял ровно посередине платформы.

Решение: Воспользуемся геометрическим методом. Будем вести отсчет в секундах. За 0 секунд примем момент, когда Иван Иванович поравнялся с началом платформы. Тогда конца платформы он достиг в момент 30 секунд. За Х сек. Обозначим момент, когда Иван Иванович выглянул в окно. Следовательно, число Х случайным образом выбирается из отрезка . С Иваном поравнялся в момент 15 секунд. Он увидел Ивана Никифоровича, только если он выглянул в окно не позже этого момента, но не раньше, чем за 10 секунд до этого. Таким образом, нужно найти геометрическую вероятность события . По формуле находим

«Вероятностная подоплека»

В самом начале поэмы «Мертвые души» два мужика спорят относительно того, как далеко доедет колесо в экипаже Чичикова:

«…два русских мужика, стоявших у дверей кабака против гостиницы, сделали кое-какие замечания, относившиеся впрочем, более к экипажу, чем к сидевшему в нем. «Вишь ты», сказал один другому: «вон какое колесо! Что ты думаешь, доедет то колесо, если б случилось, в Москву, или не доедет?» - «Доедет», отвечал другой. «А в Казань-то, я думаю, не доедет?» «В Казань не доедет», отвечал другой».

Задачи для решения.

1. Найти вероятность того, что точка случайным образом брошенная в квадрат ABCD со стороной 4 попадет в квадрат A1B1C1D1 со стороной 3, находящийся внутри квадрата ABCD.

Ответ. 9/16.

2. Два лица А и В договорились встретиться в определенном месте в промежутке времени от 900 до 1000. Каждый из них приходит наудачу (в указанный промежуток времени), независимо от другого и ожидает 10 минут. Какова вероятность того, что они встретятся?

Ответ. 11/36.

3. В отрезке АВ длины 3 случайно появляется точка С. Определить вероятность того, что расстояние от точки С до В превосходит 1.

Ответ. 2/3.

4. В круг радиусом 5 вписан треугольник наибольшей площади. Определите вероятность попадания в треугольник точки, случайно брошенной в круг.

5. Буратино посадил на прямоугольный лист размером 20 см на 25 см круглую кляксу радиусом 1 см. Сразу после этого Буратино посадил еще одну такую же кляксу, которая целиком оказалась на листе. Найдите вероятность того, что эти две кляксы не соприкасаются.

6. В окружность вписан квадрат ABCD. На этой окружности случайным образом выбирается точка М. Найдите вероятность того, что эта точка лежит на: а) меньшей дуге АВ; б) большей дуге АВ.

Ответ. а) 1/4; б) 3/4.

7. На отрезок случайным образом бросается точка Х. С какой вероятностью выполняется неравенство: а) ; б) ; в) ?

Ответ. а) 1/3; б) 1/3; в) 1/3.

8. Про село Иваново известно только, что оно находится где-то на шоссе между Миргородом и Старгородом. Длина шоссе равна 200 км. Найдите вероятность того, что:

а) от Миргорода до Иваново по шоссе меньше 20 км;

б) от Старгорода до Иваново по шоссе больше 130 км;

в) Иваново находится менее чем в 5 км от середины пути между городами.

Ответ. а) 0,1; б) 0,35; в) 0,05.

Дополнительный материал

Геометрический подход к вероятности события не зависит от вида измерений геометрического пространства: важно только, чтобы множество элементарных событий F и множество G, представляющее событие А, были бы одинакового вида и одинаковых измерений.

2. Случайная точка Х равномерно распределена в квадрате . Найти вероятность того, что квадрат с центром Х и сторонами длины b, параллельными осям координат, целиком содержится в квадрате А.

Литература:

1. Теория вероятностей и статистика / , . – 2-е изд., переработанное. – М.: МЦНМО: учебники», 2008. – 256 с.: ил.

2. Теории вероятностей и математическая статистика в примерах и задачах с применением Excel / , . – Изд. 4-е. – Ростов н/Д: Феникс, 2006. – 475 с.: ил. – (Высшее образование).

3. Пятьдесят занимательных вероятностных задач с решениями. Пер. с англ./Под ред. . 3-е изд. – М.: Наука, Главная редакция физико-математической литературы, 1985. – 88 с.

4. Сборник задач по теории вероятностей: Учеб. Пособие для вузов./, – 2-е изд., испр. И доп. – М.: Наука. Гл. ред. Физ.-мат. Лит. – 1989. – 320с.

5. Факультативный курс по математике: Теория вероятностей: Учеб. Пособие для 9-11 кл. сред. шк./ – 3-е изд. перераб. – М.: Просвещение, 1990. – 160 с.

Классическое определение вероятности имеет ограничение по его применению. Предполагается, что множество элементарных событий Ω конечно или счетное, т.е. Ω = {ω 1 , ω 2 , … , ω n , …}, а все ω i – равновозможные элементарные события. Однако, на практике встречаются испытания, для которых множество элементарных исходов бесконечно. Например, при изготовлении на станке некоторой детали нужно выдержать определенный размер. Здесь точность изготовления детали зависит от мастерства рабочего, качества режущего инструмента, совершенства станка и т.д. Если под испытанием понимать изготовление детали, то в результате такого испытания возможно бесконечное множество исходов, в данном случае получение деталей требуемого размера.

Чтобы преодолеть недостаток классического определения вероятности, иногда используют некоторые понятия геометрии (если, конечно, позволяют обстоятельства испытания). Во всех таких случаях предполагается возможность проведения (хотя бы теоретически) любого числа испытаний, и понятию равновозможности также отводится главная роль.

Пусть рассматривается испытание с пространством событий, элементарные исходы которых представляются в виде точек, заполняющих некоторую область Ω (в трёхмерном пространстве R 3). Пусть событие А состоит в попадании брошенной случайным образом точки в подобласть D области Ω. Событию А благоприятствуют элементарные события, в которых точка попадает в некоторую подобласть D . Тогда под вероятностью события А будем понимать отношение объёма подобласти D (выделенная область на рис. 1.11) к объёму области Ω, Р (А ) = V (D ) / V (Ω).

Рис. 1. 11

Здесь, по аналогии с понятием благоприятствую-щего исхода, область D будем называть благопри-ятствующей появлению события А . Аналогично определяется вероятность события А, когда множество Ω представляет собой некоторую область на плоскости или отрезок на прямой линии. В этих случаях объёмы областей заменяются соответственно площадями фигур или длинами отрезков.

Таким образом, мы приходим к новому определению ‒ геометрической вероятности для испытаний с бесконечным несчётным множеством элементарных событий, которое формулируется следующим образом.

Геометрической вероятностью события А называется отношение меры подобласти, благоприятствующей появлению этого события, к мере всей области, т.е.

р(А) = mesD / mes Ω,

где mes – мера областей D и Ω, D Ì Ω.

Геометрическая вероятность события обладает всеми свойствами, присущими классическому определению вероятности. Например, 4-е свойство будет таким: р (А + В ) = р (А ) + р (В ).

Классическое определение вероятности оказывается эффективным для решения целого спектра задач, но с другой стороны, обладает и рядом ограничений. Одним из таких ограничений является тот факт, что оно неприменимо к испытаниям с бесконечным количеством исходов. Поэтому при решении задач, в которых рассматриваются такие испытания, вместо формулы применяется другой подход, называемый геометрическим определением вероятности. На этом уроке мы познакомимся с понятием геометрической вероятности: введём определение, выясним, что оно похоже на классическое определение вероятности. Также разберём некоторые примеры на разные меры, используемые в определении геометрической вероятности (длину, площадь и объём).

2) Противотанковые мины поставлены на прямой через 15 м. Танк шириной 3 м идёт перпендикулярно этой прямой. Какова вероятность, что он подорвётся?

3) В окружность наудачу вписывается треугольник. Какова вероятность того, что он: 1) прямоугольный; 2) равнобедренный; 3) тупоугольный?

1) Виленкин Н. Я., Ивашев-Мусатов О. С. Ал-геб-ра и ма-те-ма-ти-че-ский ана-ли-з для 11 кл. Учеб.пособие для учащихся шк. и кл. с углуб. изуч. математики - М.: Просвещение, 1998.

2) Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. - М.: Дрофа.

3) М. И. Шабунин, А. А. Прокофьев, Т. А. Олейник, Т. В. Соколова. Алгебра. Начала математического анализа. Профильный уровень: задачник для 10-11 классов. — М.: БИНОМ. Лаборатория знаний, 2009.

Является понятие случайного события. Случайным событием называется событие, которое при осуществлении некоторых условий может произойти или не произойти. Например, попадание в некоторый объект или промах при стрельбе по этому объекту из данного орудия является случайным событием.

Событие называется достоверным, если в результате испытания оно обязательно происходит. Невозможным называется событие, которое в результате испытания произойти не может.

Случайные события называются несовместными в данном испытании, если никакие два из них не могут появиться вместе.

Случайные события образуют полную группу, если при каждом испытании может появиться любое из них и не может появиться какое-либо иное событие, несовместное с ними.

Рассмотрим полную группу равновозможных несовместных случайных событий. Такие события будем называть исходами. Исход называется благоприятствующим появлению события А, если появление этого события влечет за собой появление события А.

Геометрическое определение вероятности

Пусть случайное испытание можно представить себе как бросание точки наудачу в некоторую геометрическую область G (на прямой, плоскости или пространстве). Элементарные исходы - это отдельные точки G, любое событие - это подмножество этой области, пространства элементарных исходов G. Можно считать, что все точки G «равноправны» и тогда вероятность попадания точки в некоторое подмножество пропорционально его мере (длине, площади, объему) и не зависит от его расположения и формы.

Геометрическая вероятность события А определяется отношением:
,
где m(G), m(A) - геометрические меры (длины, площади или объемы) всего пространства элементарных исходов и события А.

Пример. На плоскость, разграфленную параллельными полосами шириной 2d, расстояние между осевыми линиями которых равно 2D, наудачу брошен круг радиуса r (). Найти вероятность того, что круг пересечет некоторую полосу.

Решение. В качестве элементарного исхода этого испытания будем считать расстояние x от центра круга до осевой линии ближайшей к кругу полосы. Тогда все пространство элементарных исходов - это отрезок . Пересечение круга с полосой произойдет в том случае, если его центр попадет в полосу, т.е. , или будет находится от края полосы на расстоянии меньшем чем радиус, т.е. .

Для искомой вероятности получаем: .

Относительной частотой события называют отношение числа испытаний, в которых событие появилось, к общему числу практически произведенных испытаний. Таким образом, относительная частота А определяется формулой:

(2) где m-число появлений события, n-общее число испытаний . Сопоставляя определение вероятности и относительной частоты, заключаем: определение вероятности не требует, чтобы испытания производились в действительности; определение же относительной частоты предполагает, что испытания были произведены фактически. Другими словами, вероятность вычисляют до опыта, а относительную частоту - после опыта.

Пример 2 . Из 80 случайно выбранных сотрудников 3 человека имеют серьезные нарушения сердечной деятельности. Относительная частота появления людей с больным сердцем

В качестве статической вероятности принимают относительную частоту или число, близкое к ней.

ОПРЕДЕЛЕНИЕ (статистическим определением вероятности). Число, к которому стремится устойчивая относительная частота, называется статистической вероятностью этого события.

Суммой А + В двух событий А и В называют событие, состоящее в появлении события А, или события В, или обоих этих событий. Например, если из орудия произведены два выстрела и А — попадание при первом выстреле, В — попадание при втором выстреле, то А + В — попадание при первом выстреле, или при втором, или в обоих выстрелах.

В частности, если два события А и B — несовместные, то А + В — событие, состоящее в появлении одного из этих событий, безразлично какого. Суммой нескольких событий называют событие, которое состоит в появлении хотя бы одного из этих событий. Например, событие А + В + С состоит в появлении одного из следующих событий: А, В, С, А и В, А и С, В и С, А и В и С. Пусть события A и В — несовместные, причем вероятности этих событий известны. Как найти вероятность того, что наступит либо событие A, либо событие В? Ответ на этот вопрос дает теорема сложения.

Теорема. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

Р (А + В) = Р (А) + Р (В). Доказательство

С л е д с т в и е. Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

Р (A 1 + A 2 + ... + A n) = Р (A 1) + Р (A 2) + ... + Р (A n).

ТВ Случайным явлением

1. Классический

2. Стохастический основным факторам второстепенным

Событием

Различают достоверное невозможное случайное

Свойства вероятности:

<Р(С)<1.

Два события А и В называются несовместными совместными

единственно-возможными

полную группу

противоположными .

Под отрицанием

частоте данного события

Теорема Бернулли по вероятности

Достоинством

Недостатками

Вероятность события

комбинаторики .

Сочетаниями из n по m называются соединения, состоящие из n элементов и отличающиеся друг от друга составом элементов. Число сочетаний из n по m равно числу способов выбора m элементов из имеющихся n: , где n>m.

сочетаниями с повторениями : .

Размещениями

размещениями с повторениями : .

Перестановками

Основные понятия мат.статистики

Аналогом СВ из теории вероятности является признак Х в мат.статистике.

Множество всевозможных значений признака Х, позволяющее оценить параметры распределения, а также само распределение признака Х с исчерпывающей точностью, называют генеральной совокупностью.

Выборкой признака Х называют ограниченный объем стат.данных генеральной совокупности: ; - элементы выборки, n – объем выборки

Отбор выборочных данных из ген.совокупности – акт случайности ⇒ выборку можно рассмотреть как многомерную СВ. Значит, каждый элемент выборки – это СВ.

Закон распределения выборки и её элементов совпадает с законом распределения ген.совокупности, их которых она извлечена.

Основным св-ом выборки является её случайность. Это обеспечивает репрезентативность (представительность) выборки. В противном случае говорят об ошибке – презентативности.

Точечная оценка параметров распределения. Требования к функциям выборки.

Функцией выборки называется нек-я ф-ция, переводящая элементы выборки в числовое значение. Функция выборки используется для оценки параметров распределения, границ доверительного интервала и оценки статистики критерия. Т.к.элементы выборки случайны, то число полученное по функции выборки- также величина случайная. Точечной оценкой Qn (с тильдой наверху) параметра распределения Q наз-ся величина, характеризующая истинное значение параметра Q. Для оценки одного и того же параметра распределения можно составить несколько различных функций выборки. Требования : 1.состоятельности -оценка параметра при n стремящимся к бесконечности сходится по вероятности к истинному значению этого параметра. Записывается так и так . 2.несмещенности - мат.ожидание оценок параметров распределения = истинному значению этого параметра. Если это равенство выполняется прия любых n, то это абсолютная несмещенность; а если при n стремящемся к бесконечности то асимптотическая. 3.эффективности - эффективной называют ту функцию выборки (оценку), к-я обладает наименьшей дисперсией. , где в числителе -дисперсия исследуемой оценки, в знаменателе -дисперсия эффективной оценки. Чем ближе коэффициет эффективности e к 1, тем эффективнее исследуемая оценка. Если это условие выполняется при n стремящемся к бесконечности, то это ассимптотическая эффективность.

Гистограмма распределения.

Первое, что можно получить из всякой конкретной выборки Х=(х 1 ,х 2 ,…,х n) – это начальное представление о законе распр-я. Осуществляется это путем построения так называемой гистограммы распр-я. Для этого опр-ся диапазон изменения возможных значений исследуемого признака (аналог СВ в ТВ) по имеющейся выборке Х=(х 1 ,х 2 ,…,х n) – от x’=min{x i } до x”= max{x i }. Этот диапазон условно подразделяется на М интервалов – так называемых разрядов, или «карманов» гистограммы. Число М выбирается исследователем. Согласно формуле Стерджеса рекомендуемое число М интервалов разбиения M . Если выбрать все разряды одинаковыми по ширине, то ширина разряда будет равняться: h= .

Затем для i-го разряда (i=1,2,…,M) подсчитывается число m i попавших в него значений СВ. Полученные значения m i или откладываются в масштабе по вертикали применительно к каждому разряду. Полученная таким образом гистограмма получила название гистограммы распределения признака Х:

На основе гистограммы получаем первичное представление о виде закона распр-я исследуемого признака. При этом выполняются условия: ; .

Предмет теории вероятностей. Основные понятия.

ТВ - раздел математики, занимающийся изучением закономерностей в массовых случайных явлениях. Случайным явлением называют явление, обладающее след. свойствами: неопределенности исхода, возможности воспроизведения, возможности измерения исхода каждого события.

Для изучения случайных явлений используются 2 подхода:

1. Классический (детерменистский): закономерности случайных явлений определяются по основным факторам, чаще всего применяется в естественнонаучных исследованиях. Пренебрежение второстепенными факторами приводит к появлению элемента случайности в исследуемых явлениях.

2. Стохастический : используется в социально-экономических исследованиях, закономерности случайных явлений определяются как по основным, так и по второстепенным факторам. Полный учёт второстепенных факторов практически невозможен, поэтому результаты исследований носят вероятностный характер. К основным факторам относятся факторы, оказывающие сущ-ое влияние на исход испытания. К второстепенным относятся факторы с незнач. влиянием на исход испытания.

Элемент случайности в явлениях снижается: при воспроизведении большего числа второстепенных факторов, с ростом массовых явлений.

Событием называется всякий факт, который может (не)произойти при выполнении определенного комплекса условий (А, В,..., А 1 , А 2).

Различают достоверное (событие, которое наступает обязательно при выполнении комплекса условий), невозможное (событие, которое не может наступить при выполнении определенного комплекса условий) и случайное (все остальные события) событие.

Вероятностью события называется численная мера объективной возможности наступления этого события (Р(А), р 1 ,...).

Свойства вероятности:

вероятность достоверного события равна 1: Р(А)=1;

вероятность невозможного события равна 0: Р(В)=0;

вероятность случайного события определяется: 0<Р(С)<1.

Два события А и В называются несовместными (или), если наступление одного из них исключает наступление другого. События называются совместными (и), если они могут появиться одновременно в одном испытании.

События А 1 , А 2 ,...,А n называются единственно-возможными , если в результате испытания наступает хотя бы одно из этих событий.

События А 1 , А 2 ,...,А n образуют полную группу событий, если являются возможно-несовместными и единственно-возможными.

Два события, образующие полную группу называются противоположными .

Под отрицанием события понимают наступление противоположного события: А, .
2. Относительная частота события. Теорема Бернулли.

Вероятности событий, эксперименты по воспроизведению которых не обладают свойством симметрии исходов, определяются по частоте данного события или статистической вероятностью этого события.

Статистической вероятностью события А называется отношение числа экспериментов, в которых событие наступило, к общему числу экспериментов: W(A)=P*(A)=m/n, где n-общее число экспериментов, m-число, в которых наступило событие А.

Статистическая вероятность события - лишь оценка истинного значения вероятности этого события. Её использование возможно при выполнении след. условий:

1. Должны существовать возможности многократного воспроизведения экспериментов на предмет наступления события А при определенных условиях.

2 События должны обладать статистической устойчивостью или устойчивостью относительных частот.

3. Число экспериментов должно быть достаточно велико.

Теорема Бернулли : С ростом числа экспериментов, т.е. при n→¥, относительная частота события сходится по вероятности к истинному значению вероятности этого события: , .

Достоинством частотной схемы определения вероятности является широкий класс решаемых задач.

Недостатками являются: приближенное значение вероятности события; большие моральные, материальные и временные затраты для получения этой оценки.
3. Классическое определение вероятности события. Формулы комбинаторики.

Вероятность события - эксперимент, по воспроизведению которого можно разложить на равновозможные исходы равна: Р(А)=m/n, где n-общее число возможных исходов, m-число исходов, благоприятствующих событию А.

Для нахождения значения m и n используют формулы комбинаторики .

Если в сочетаниях выбираемые элементы могут повторяться, то их называют сочетаниями с повторениями : .

Размещениями из n по m называются соединения, состоящие из m элементов и отличающиеся друг от друга либо составом элементов, либо порядком их следования: .

Если в размещениях элементы могут повторяться, то их называют размещениями с повторениями : .

Перестановками из n элементов называются соединения, состоящие из n элементов, и отличающиеся друг от друга порядком следования элементов: .

Геометрическое определение вероятности события.

В случаях, когда исходы испытания равняются равновозможными, а их число бесконечным множеством, вероятность некоторых событий можно определить как отношение меры благоприятствующей области к мере области, т.е. P(A)=m(G)/n(S).

В качестве меры областей может выступать длина отрезка, площадь плоской фигуры или объем тела.

Вся область S и благоприятствующая область G должны быть замкнутыми и измеримыми.

Рассмотрим плоскую фигуру S, внутри которой появляется случайная точка. Выделим подобласти S 1 и S 2 . Событие A - случайно выбранная точка, окажется внутри заштрихованных областей S 1 и S 2 . P(A)=(S 1 +S 2)/S.
5. Совместные и несовместные события. Теорема сложения вероятностей.

Если одно из событий произойдет обязательно, то такие события образуют полную группу событий.

Суммой 2-х событий А и В называется событие С, состоящее в наступлении либо события А, либо события В: С=А+В.

Произведением 2-х событий А и В называется событие С, состоящее в совместном наступлении как события А, так и В: С=A×B.

Под отрицанием события А понимают наступление противоположного ему события: .

Теорема сложения совместных событий : Вероятность суммы 2-х совместных событий равна сумме вероятностей этих событий без вероятности их совместного наступления: P(A+B)=P(A)+P(B)–P(A×B).

□ Пусть n-общее число возможных исходов, из них m способствуют наступлению события А, k благоприятствует событию В, l-число исходов, способствующих совместному наступлению А и В:

Р(А)=m/n, Р(В)=k/n, P(A×B)=l/n, А+В→m+k-l.

Р(А+В)=(m+k-l)/n=m/n+k/n–l/n= P(A+B)=P(A)+P(B)–P(A×B)■.

Теорема сложения несовместных событий : Вероятность суммы 2-х несовместных событий равна сумме вероятностей этих событий: P(A+B)=P(A)+P(B).

□ Т.к. А и B–несовместные события, то A×B–невозможное событие:

P(A+B)=P(A)+P(B)–0=P(A)+P(B)■.

Следствие 1 : Сумма вероятностей событий, образованных полную группу событий=1: Р(А 1 , А 2 ,...,А n)=1.

□ Т.к. А 1 , А 2 ,...,А n образуют полную группу событий, то они попарно несовместно и является единственно возможными, тогда А 1 , А 2 ,...,А n –достоверное событие:

Р(А 1 , А 2 ,...,А n)= Р(А 1)+Р(А 2)+...+Р(А n)=1■.

Следствие 2 : Вероятность суммы противоположных событий=1: Р(А+ )=Р(А)+Р()=1.
6. Зависимые и независимые события. Теорема умножения вероятностей.

Два события А и В называются зависимыми , если вероятность наступления одного из них зависит от наступления другого события, в противном случае события независимые (если появление одного из событий не влияет на вероятность появления другого).

Под условной вероятностью события А понимают вероятность этого события, вычисленную при условии, что событие В наступило: Р(А/В), Р В (А).

Теорема (зависимость события) умножения : Вероятность произведения 2-х зависимых событий равна произведению вероятности одного из них на условную вероятность другого события: P(A×B)=Р(А)×Р(В/А)=Р(В)×Р(А/В).

□ Пусть n-общее число возможных исходов, из них m благоприятствуют событию А, k-событию В, l-одновременно событию А и В:

Р(В/А)=l/m=(l/n)/(m/n)= P(A×B)/Р(А)=> P(A×B)=Р(А)×Р(В/А).

1 из m исходов наступил 1/m (событие А наступило), из этих m исходов l способствуют наступлению события:

Р(А/В)=l/k=(l/n)/(k/n)= P(A×B)/P(B)=> P(A×B)=Р(В)×Р(А/В)■.

Для n зависимых событий теорема умножения вероятностей примет вид:

Р(А 1 ×А 2 ×...×А n)=Р(А 1)×Р(А 2 /А 1)×Р(А 3 /А 1 ×А 2)×...×Р(А n /А 1 ×А 2 ×...×А n -1).

Р(А)=Р(А/В)=> А 1 ×В -независимые события, Р(А)≠Р(А/В)=> А 1 ×В -зависимые события.

7. Полная группа событий. Формула полной вероятности:

Набор событий H1, H2, …, Hn называется полной группой попарно несовместных событий если:

Пусть мы имеем полную группу несовместных событий H1, H2, …, Hn, определяющих варианты условий, в которых может осуществляться опыт по воспроизведению некоторого события А. Каждой гипотезе будет соответствовать своя условная вероятность события А: P(A/Hi), i=1,2,…,n.

Теорема: Если H1,H2,…,Hn – полная группа попарно несовместных событий, причем P(Hi) 0, i=1,2,…,n,то для любого события А имеет место равенство:

- формула полной вероятности.

8. Формула Байеса переоценки вероятностей гипотез. Ее практическое значение.

Одним из самых важных следствий формулы полной вероятности является формула Байеса.

, i=1,2,…,n.

Используя формулу Байеса, мы оцениваем вероятность того, какая из возможных причин в действительности имела место при условии, что событие А произошло.

Вероятности при -априорные вероятности. -апостериорные вероятности. Процесс решения задач по формуле полной вероятности и формуле Байеса можно представить виде граф.схемы типа дерева, кот имеет одну корневую и несколько корневых вершин, соединенных м/у собой звеньями.

9. Формула Бернулли и Пуассона:

Теорема Бернулли: если вероятность p наступления события А в каждом испытании постоянна, то вероятность Pm,n того, то событие А наступит m раз в n независимых испытаниях Бернулли, равна:

, где q=1-p.

Формула Бернулли применяется при сравнительно небольших m и n.

Теорема Пуассона: Если вероятность p наступления события А в каждом испытании стремиться к 0 (p->0) при неограниченном увеличении числа n испытаний (n-> )/. Причем произведение np стремится к постоянному числу (), то вероятность того,что событие А появиться m раз n независимых испытаниях удовлетворяет предельному равенству.

Главная » Кардиология » Задачи с решениями. Геометрическое определение вероятности. Задачи с решениями